เซต คือ กลุ่มของสิ่งต่างๆ
เรียกสิ่งที่อยู่ในเซต ว่า สมาชิก
นิยมแทนเซตด้วยอักษรตัวใหญ่ เช่น A ,B ,C, D…
และเขียนสมาชิกของเซตให้อยู่ใน {} (วงเล็บปีกกา)
หากมีสมาชิกมากกว่า 1 ตัว ให้ใช้ , คั่น
เราจะเขียนชื่อ เซต = {สมาชิก}
เครื่องหมาย
หมายถึง เป็นสมาชิก
หมายถึง ไม่เป็นสมาชิก
ตัวอย่าง
ถ้า A คือเซตของวันใน 1 สัปดาห์
จะได้ A = {วันอาทิตย์,วันจันทร์,วันอังคาร,วันพุธ,วันพฤหัสบดี,วันศุกร์,วันเสาร์}
ซึ่งเซต A มีสมาชิก 7 ตัว คือ
วันอาทิตย์ ∈ A (วันอาทิตย์ เป็นสมาชิกของเซต A)
วันจันทร์ A
วันอังคาร A
วันพุธ A
วันพฤหัสบดี A
วันศุกร์ A
วันเสาร์ A
มกราคม A (มกราคม ไม่เป็นสมาชิกของเซต A)
การเขียนเซต
สามารถเขียนได้ 2 แบบ 1. แบบแจกแจงสมาชิก และ 2 . แบบบอกเงื่อนไข
แบบแจกแจงสมาชิก คือ เราสามารถทราบได้เลยว่ามีสมาชิกกี่ตัว เช่น
A = {3,5,7,9}
จะได้ว่า
3 A
5 A
7 A
9 A
2 A
4 A
แบบบอกเงื่อนไข เช่น
B = { B (เป็นสมาชิกของเซตB เพราะ มากกว่า 2 และ เป็นจำนวนคู่)
6 B (เป็นสมาชิกของเซตB เพราะ มากกว่า 2 และ เป็นจำนวนคู่)
100 B (เป็นสมาชิกของเซตB เพราะ มากกว่า 2 และ เป็นจำนวนคู่)
2020 B (เป็นสมาชิกของเซตB เพราะ มากกว่า 2 และ เป็นจำนวนคู่)
2 B (ไม่เป็นสมาชิกของเซตB เพราะ ต้องมากกว่า 2 และ เป็นจำนวนคู่)
321 B (ไม่เป็นสมาชิกของเซตB เพราะ มากกว่า 2 แต่ไม่เป็นจำนวนคู่)
จำนวนสมาชิก
จำนวนสมาชิกของเซต A สามารถเขียนแทนด้วย n(A) หรือ โดยที่ตัว A สามารถเปลี่ยนเป็นอย่างอื่นได้ ถ้าเป็นสมาชิกของเซต B เราก็สามารถเขียนได้ว่า n(B) หรือ
เซตที่มีจำนวนสมาชิกมากจนไม่สามารถนับได้ เรียกว่า เซตอนันต์ เช่น จำนวนเม็ดทราย
เซตที่สามารถนับจำนวนสมาชิกได้ เรียกว่า เซตจำกัด เช่น จำนวนนักเรียนภายในห้อง
เซตที่มีจำนวนสมาชิก 0 ตัว เรียกว่า เซตว่าง สามารถเขียนแทนด้วย {} ,
สัญลักษณ์ที่ควรทราบ
เซตของจำนวนนับ ได้แก่ 1,2,3,4,…..
หรือ
เซตของจำนวนเต็ม ได้แก่ ….. , -3,-2,-1,0,1,2,34,….
เซตของจำนวนเต็มบวก(เหมือน
) ได้แก่ 1,2,3,4,5,…..
เซตของจำนวนเต็มศูนย์ ได้แก่ 0
เซตของจำนวนเต็มลบ ได้แก่ -1,-2,-3,-4,-5,….
เซตของจำนวนตรรกยะ (เขียนในรูป
ได้) (จำนวนเต็ม Integer)
ได้แก่ 5 , ,
,
,
เซตของจำนวนอตรรกยะ (เขียนในรูป
ไม่ได้)
ได้แก่ ,
,
,
เซตจำนวนจริง
ได้แก่
,
,
,
U เอกภพสัมพัทธ์ คือ ขอบเขตที่เราสนใจ
หากโจทย์ไม่ได้กำหนดจะถือว่าเอกภพสัมพันธ์เป็นเซตที่ใหญ่ที่สุด คือ จำนวนจริง
การเท่ากันของเซต
เซตจะเท่ากันก็ต่อเมื่อมีจำนวนสมาชิกเท่ากันและจำนวนสมาชิกต้องเหมือนกันทุกตัว
โดยจะเรียงแบบไหนก็ได้ ซึ่งสมาชิกที่ซํ้ากันจะนับแค่ครั้งเดียวเท่านั้น
ตัวอย่าง
ให้
A=B หรือไม่?
เซต A ไม่เท่ากับเซต B เพราะถึงแม้ว่าจำนวนสมาชิกจะเท่ากัน แต่สมาชิกภายในเซตบางตัวไม่เหมือนกัน
A=C หรือไม่?
เซต A เท่ากับเซต C เพราะมีจำนวนสมาชิกเท่ากันและสมาชิกภายในเซตทุกตัวเหมือนกัน
สับเซต
หมายถึง เป็นสับเซต
หมายถึง ไม่เป็นสับเซต
A เป็นสับเซตของ B เขียนแทนด้วย
หมายความว่าสมาชิกทุกตัวในเซต A เป็นสมาชิกในเซต B
เซตว่าง เป็นสับเซตของ ทุกเซต เซตทุกเซตจะเป็นสับเซตของตัวมันเอง
ตัวอย่าง
จงหาสับเซตทั้งหมดของ D = {ก,ข}
ตอบ สับเซตทั้งหมดของ D คือ , {ก} , {ข} , {ก,ข}
A = {2 , 4 , 6} และ B = {1 , 2 , 3, 4 , 5 , 6] เพราะสมาชิกทุกตัวในเซต A เป็นสามาชิกในเซต B
C = {1 , 2 , 7} และ B = {1 , 2 , 3 , 4 , 5 , 6} เพราะสมาชิกบางตัวในเซต C ไม่เป็นสมาชิกในเซต B
จำนวนสมาชิกในเซต คือ n(A)
จำนวนสับเซตคือ 2n(A) คือการเอา 2 มายกกำลังกับ จำนวนสมาชิกของเซตนั้น เช่น D = {ก,ข} เซต D มีสมาชิก 2 ตัว ดังนั้นสับเซตของเซต B จะเท่ากับ 22 = 4 ดังนั้นสับเซตของเซต B จะต้องมีสมาชิกทั้งหมด 4 ตัว
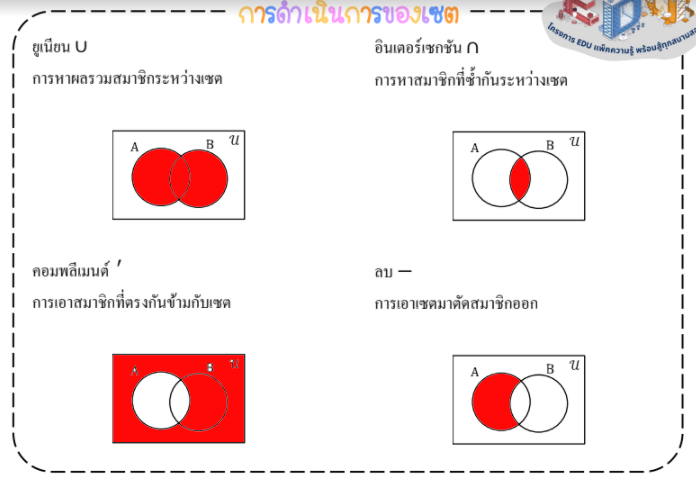
การดำเนินการของเซต
เพาเวอร์เซต
คือ เซตของสับเซตทั้งหมด
เพาเวอร์เซตของ A เขียนแทนด้วย P(A) ซึ่งทุกเพาเวอร์เซตจะมี และตัวมันเองเป็นสมาชิก
สรุปง่ายๆ เพาเวอร์คือการเอา สับเซตทั้งหมดมาใส่ในเซต { สับเซตทั้งหมด }
ตัวอย่าง
ให้ D = {ก,ข}
สับเซตทั้งหมดของ D คือ , {ก} , {ข} , {ก,ข}
ดังนั้น P(D) = {, {ก} , {ข} , {ก,ข} }
ควรรู้
{a , b} P(A) หมายความว่า { a , b }
A
{ a , b } A หมายความว่า a
A และ b
A
ถ้า a , b เป็นสมาชิกของสับเซต A หมายความว่า a , b ต้องเป็นสับเซตในเซต A ด้วย
คือ a ต้องเป็นสมาชิกใน A และ b ต้องเป็นสมาชิกใน A ด้วย
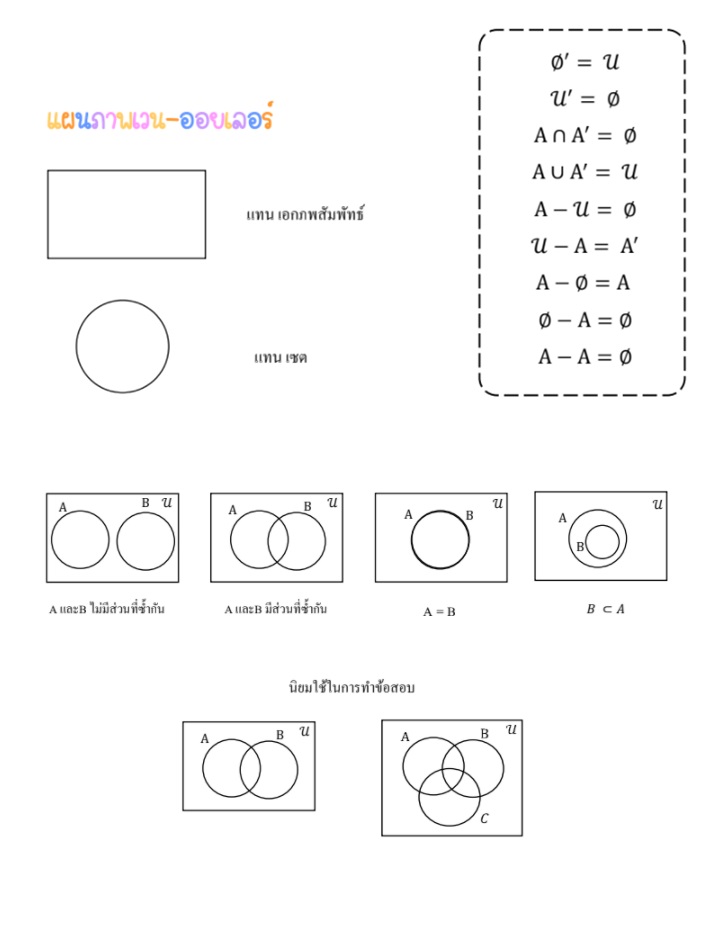
โจทย์เรื่องเซต
โรงเรียนแห่งหนึ่งสำรวจความชอบของนักเรียนที่เข้าร่วมกิจกรรมค่าย ซึ่งประกอบด้วยฐานวิทยาศาสตร์ และ ฐานคณิตศาสตร์ พบว่า
มีนักเรียนร้อยละ 9 ไม่ชอบกิจกรรมทั้งสองฐาน
มีนักเรียนร้อยละ 61 ชอบกิจกรรมฐานวิทยาศาสตร์
มีนักเรียนร้อยละ 35 ชอบกิจกรรมทั้งสองฐาน
ถ้ากลุ่มนักเรียนที่เข้าร่วมกิจกรรมค่ายนี้มา 1 คน แล้วความน่าจะเป็นที่นักเรียนคนนี้ชอบกิจกรรมฐานคณิตศาสตร์เท่ากับเท่าใด
ฐานวิทยาศาสตร์ คือ เซต A
ฐานคณิตศาสตร์ คือ เซต B
(เอกภพสัมพัทธ์) U = 100 (100 เอามาจากร้อยละ)
มีนักเรียนร้อยละ 9 ไม่ชอบกิจกรรมทั้งสองฐาน
U = 100 – 9 = = 91
มีนักเรียนร้อยละ 61 ชอบกิจกรรมฐานวิทยาศาสตร์ = n(A) = 61
มีนักเรียนร้อยละ 35 ชอบกิจกรรมทั้งสองฐาน = = 35
n(A) – = 26
ความน่าจะเป็นที่นักเรียนคนนี้ชอบกิจกรรมฐานคณิตศาสตร์เท่ากับเท่าใด = n(B)
– n( A – B ) = n(B)
91 – 26 = 65
ความน่าจะเป็น
ให้ A , B และ C เป็นเซตใดๆ พิจารณาข้อความต่อไปนี้
(ก) ถ้า และ
แล้ว
(ข)
(ค) ถ้าเซต A มีสมาชิก 9 ตัว เซต B มีสมาชิก 7 ตัว และ เพาเวอร์เซตของเซต A – B สมาชิก 32 ตัว แล้วเพาเวอร์เซตของเซต B – A มีสมาชิก 16 ตัว
ข้อใดถูกต้อง
1 ข้อ (ก) และ ข้อ (ข) ถูก แต่ ข้อ (ค) ผิด
2 ข้อ (ก) และ ข้อ (ค) ถูก แต่ ข้อ (ข) ผิด
3 ข้อ (ข) และ ข้อ (ค) ถูก แต่ ข้อ (ก) ผิด
4 ข้อ (ก) และ ข้อ (ข) และ ข้อ (ค) ถูกทั้งสามข้อ
5 ข้อ (ก) และ ข้อ (ข) และ ข้อ (ค) ผิดทั้งสามข้อ
(ก) ถ้า และ
แล้ว
แสดงว่าเซต B และ เซต C ต้องไม่มีสมาชิกร่วมกัน จึงกำหนดเซต
B = {1} , C = {2} , A = {1}
A เป็นสับเซตของ
แสดงว่า A จะเป็นเซต 1 หรือ 2 หรือ 1,2 ก็ได้ จึงกำหนดให้ A = {1}
ไม่มีสมาชิกร่วมกันจึงได้เซตว่าง
เซตว่างมีค่าเท่ากับเซตของ 1 จริงมั้ย ไม่จริง เพราะว่าเซตว่างมีจำนวนสมาชิกเท่ากับ 0 ตัว
ดังนั้นข้อ ก. ผิด
(ข)
โจทย์ที่เป็นสับเซตเราจะตรวจสอบว่ามันเป็นจริงหรือเปล่า เราก็ต้องกำหนดเซตสมาชิกของเซตให้มันขัดแย้งกับโจทย์
กำหนดให้ , A = {1} , C = {2}
{1}
เซตของ 1 เป็นสับเซตของเซตว่างจริงมั้ย ไม่จริง เพราะเซตว่างไม่มีสมาชิก
ดังนั้นข้อ ข. ผิด
(ค) ถ้าเซต A มีสมาชิก 9 ตัว เซต B มีสมาชิก 7 ตัว และ เพาเวอร์เซตของเซต A – B สมาชิก 32 ตัว แล้วเพาเวอร์เซตของเซต B – A มีสมาชิก 16 ตัว
ถ้าเซต A มีสมาชิก 9 ตัว n(A) = 9
เซต B มีสมาชิก 7 ตัว n(B) = 7
เพาเวอร์เซตของเซต A – B สมาชิก 32 ตัว n(P(A – B)) = 32
สูตรคำนวณจำนวนคร่าวๆเพาเวอร์เซต
ยกตัวอย่าง
n(A) = 9
n(P(A)) =เอา 2 ยกกำลังกับ n(A) ส่วน 9 ด้านบนมาจากจำนวนสมาชิกของเซตนั้นๆ
n(P(A – B)) = 32 = 25
n(A-B) = 5
n(B-A) = 3
n(P(B-A)) = 2n(ฺB-A)
= 23 = 8
ดังนั้นข้อ (ค.) เพาเวอร์เซตของเซต B – A มีสมาชิก 16 ตัว ผิด

ให้ และ
ให้่ และ
เป็นโดเมน และเรนจ์ของ
ตามลำดับ พิจารณาข้อความต่อไปนี้
(ก) เป็นฟังก์ชัน
(ข) จำนวนสมาชิกของเซต เท่ากับ 3
(ค)
ข้อใดถูกต้อง
1. ข้อ (ก) ถูกเพียงข้อเดียว
2. ข้อ (ข) ถูกเพียงข้อเดียว
3. ข้อ (ค) ถูกเพียงข้อเดียว
4. ข้อ (ก) ข้อ (ข) ข้อ (ค) ถูกทั้งสามข้อ
5. ข้อ (ก) ข้อ (ข) ข้อ (ค) ผิดทั้งสามข้อ
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 1 | 0 | -1 | -2 | -1 | 0 | 1 |
= 1
= 0
= -1
= -2
= -1
= 0
= 1
จับคู่ลำดับ x , y
r = { (-3 , 1) , (-2 , 0) , (-1 , -1) , (0 , -2) , (1 , -1) , (2 , 0) , (3 , 1) }
r-1 = { (1 , -3) , (0 , -2) , (-1 , -1) , -2 , 0) , (-1 , 1) , (0 , 2) , (1 , 3) }
มีการซํ้ากันในค่า y ฉะนั้นข้อ (ก) เป็นฟังก์ชัน จึงผิด
*การที่มันจะเป็นฟังก์ชันได้ ก็แสดงว่า x จะต้องมีคู่อันดับ y เพียงตัวเดียว
(ข) จำนวนสมาชิกของเซต เท่ากับ 3
มาดูว่า มีสมาชิกตัวไหนที่มันมีทั้งใน r และ r-1
r = { (-3 , 1) , (-2 , 0) , (-1 , -1) , (0 , -2) , (1 , -1) , (2 , 0) , (3 , 1) }
r-1 = { (1 , -3) , (0 , -2) , (-1 , -1) , (-2 , 0) , (-1 , 1) , (0 , 2) , (1 , 3) }
แสดงว่า (ข) จำนวนสมาชิกของเซต เท่ากับ 3 ถูกต้อง เพราะว่า พอเอามาอินเตอร์เซกกันแล้วมีสมาชิกเท่ากับ 3
(ค)
r = { (-3 , 1) , (-2 , 0) , (-1 , -1) , (0 , -2) , (1 , -1) , (2 , 0) , (3 , 1) }
r-1 = { (1 , -3) , (0 , -2) , (-1 , -1) , (-2 , 0) , (-1 , 1) , (0 , 2) , (1 , 3) }
= {-3 , -2 , -1 , 0 , 1 , 2 , 3}
= {1 , 0 , -1 , -2 } *ส่วน -1 , 0 , 1 เราจะไม่ใส่ซํ้ากัน
พอเอามาอินเตอร์เซก จะมีแค่ 1 , 0 , -1 , -2 ซึ่งมันไม่เท่ากับเซทของ
ดังนั้น ประโยค จึงผิด
ให้ n(S) แทนจำนวนของเซต S ถ้า A , B และ C เป็นเซต โดยที่ n(A) + n(B) + n(C) = 199
และ
แล้ว เท่ากับข้อใดต่อไปนี้
1. 42
2. 43
3. 44
4. 45
5. 46
สูตร



หาสมาชิกในเซต C
100 – 35 = n(C) = 65
n(A) + n(B) + n(C) = 199
n(A) + n(B) + 65 = 199
n(A) + n(B) = 199 – 65
= 134
หาได้จากการเอารูปที่ 1 มา ลบ กับรูปที่ 3
100 – 9 = = 91
91 = 134 – = 134 – 91
= 43
กำหนดให้ และให้ A และ B เป็นสับเซตของ U โดยที่
และ
จำนวนสมาชิกของ A×B เท่ากับเท่าใด
U = {1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10}
n(A) x n(B) = ?
U = {1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10}

และ
U = {1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10}

U = {1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10}

U = {1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10} เหลือ 2 ,4, 8, 10 อยู่ในเซต A

n(A) = 6
n(B) = 4
ดั้งนั้น n(A) x n(B) = 6 × 4 = 24
สอนโดย : edu.pack_forexam
10 เรื่องจริง Everest
10 เรื่องจริง Pentagon เพนตากอน
10 เรื่องจริง มาริโอ้ Mario
10 เรื่องจริงของ ความฝัน Dream
10 เรื่องจริงของ ทองคำ Gold
10 เรื่องจริงของแมว Cat
10 สิ่งประดิษฐ์เปลี่ยนโลก
10 สถิติ ที่ยังไม่ถูกทำลาย